К истории закона сохранения количества движенияПонятие количества движения как специальной механической величины, выражающейся произведением массы тела на скорость его движения, ввел Ньютон в "Математических началах натуральной философии". Количество движения связывалось вторым законом динамики с силой, изменение количества движения служило мерой силы. С другой стороны, произведение массы на скорость рассматривалось как мера движения. Закон сохранения количества движения появился впервые именно при рассмотрении мер движения. Первая формулировка принадлежит Декарту. В своем основном труде "Начала философии", вышедшем в 1644 году, Декарт развивает мысль о том, что Вселенная заполнена различными формами движущейся материи. Первопричиной движения он считает бога и дает следующую теологическую формулировку закона сохранения: "Бог - первопричина движения, он постоянно сохраняет в мире одинаковое его количество". Декарт не дал математического выражения закона. Он лишь наметил первый шаг в следующей формулировке: "Когда одна частица материи движется вдвое скорее другой, а эта последняя вдвое по величине больше первой, то в меньшей столько же движения, сколько и в большей из частиц; и что насколько движение одной частицы замедляется, настолько же движение какой-либо иной возрастает". Далее смысл закона не проясняется, а, наоборот, запутывается. Лейбниц начал дискуссию о мере движения в работе с интересным названием "Краткое доказательство замечательного заблуждения Декарта и других в вопросе об одном законе природы, по которому, как они полагают, благодаря Господу сохраняется всегда одно и то же количество". Лейбниц считает мерой движения не произведение массы на скорость 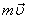 , а произведение , а произведение  . Он делает первый шаг к открытию закона сохранения энергии, но безнадежно запутывает вопрос о соотношении законов сохранения количества движения и энергии. Эта путаница бытовала более 100 лет и мешала прояснению закона сохранения энергии. . Он делает первый шаг к открытию закона сохранения энергии, но безнадежно запутывает вопрос о соотношении законов сохранения количества движения и энергии. Эта путаница бытовала более 100 лет и мешала прояснению закона сохранения энергии. Развитие ньютоновской динамики привело к выяснению связи между законами динамики и законом сохранения количества движения. Для одного тела  . При отсутствии внешних сил . При отсутствии внешних сил 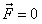 , ,  и сразу же следует сохранение количества движения: и сразу же следует сохранение количества движения: 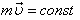 . В случае постоянной массы . В случае постоянной массы  мы приходим к первому закону динамики. мы приходим к первому закону динамики. Рассматривая замкнутую систему взаимодействующих тел, можно написать 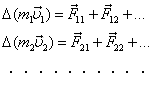
Суммируя правые и левые части и пользуясь третьим законом динамики, согласно которому 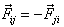 , получаем , получаем 
|