Малый поршень гидравлического пресса за один ход опускается на расстояние h₁ = 0,2 м, а большой поршень поднимается на высоту h₂ = 0,01 м. С какой силой F₂ действует пресс на зажатое в нем тело, если на малый поршень действует сила F₁=500Н?

Дано: F2 - ?	Решение
h1 = 0,2 м h2 = 0,01 м F1 = 500Н

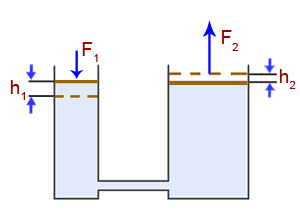Действие гидравлического пресса основано на законе Паскаля. Выигрыш в силе, который дает пресс определяется отношением площадей его поршней, т. е:

где S₁ - площадь малого поршня, S₂ - площадь большого поршня.

В задаче неизвестны площади поршней. Однако даны расстояния, на которые они смещаются. Попробуем найти связь между площадями поршней и данными расстояниями.

Левая и правая части пресса имеют цилиндрическую форму, а объем цилиндра равен произведению площади его основания на высоту (т. е. hS). Заметим, что жидкость, которой заполнен пресс, можно считать несжимаемой. Тогда объем жидкости вытесненный из левого колена, равен объему, прибавившемуся в правом, т. е.:
h₁S₁ = h₂S₂

Откуда

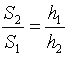
Значит,
, или

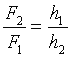
Из последнего уравнения выразим F₂
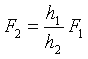