Задачи на уравнение теплового баланса.
В калориметр, содержащий 500 г воды при температуре 20°С, кладут кусок льда при температуре 0°С. Какая наименьшая масса льда нужна для того, чтобы температура содержимого калориметра стала равной 0°С?
Дано:
mл - ?
|
Решение |
|
mв = 500 г = 0,5 кг
t1в = 0°С
t2в = 0°С
cв = 4200 Дж / кг •°C
λл = 3,3 • 105 Дж / кг
|
Процесс проходит в идеальном калориметре, поэтому теплообмен идет между водой и льдом. Составим уравнение теплового баланса:
Qв + Qл = 0.
Qв = cmв(t2в - t1в) - количество теплоты, отданное водой
Лед взят при температуре плавления, значит
Qл = λлmл - количество теплоты, полученное льдом.
Поэтому:
cmв(t2в - t1в) + λлmл = 0
λлmл = - cmв(t2в - t1в), или λлmл = cmв(t1в - t2в)
|
Мальчик наполнил стакан на ¾ кипятком и дополнил его холодной водой. Определите, какая установилась температура воды, если температура холодной воды равна 20°С. Теплоемкость стакана и потери тепла не учитывайте.
Дано:
t2cм - ?
|
Решение |
t1г = 100 °С
t1х = 20 °С
|
Составим уравнение теплового баланса. В теплообмене участвуют два тела – холодная и горячая вода. Значит
Qг + Qх = 0
Заметим, что в условии задачи нет данных для массы тел. Однако известно, что стакан заполнен на ¾ кипятком. Значит,
Vг = ¾V, тогда Vх = ¼V.
Поэтому
mг = ¾Vρ и mх = ¼Vρ.
|
Из уравнения теплового баланса имеем:
cmх(t2cм – t1х ) = - cmг(t2cм – t1г )
¼Vρc (t2cм – t1х ) = ¾Vρcв (t1г - t2cм).
Откуда (t2cм – t1х ) = 3 ( t1г - t2cм)
4t2cм = 3t1г + t1х
Сколько нужно смешать горячей воды , имеющей температуру 80 °С, и холодной, имеющей температуру 20 °С, чтобы получить 60 кг воды с температурой 40 °С.
Дано:
mг - ?
mх - ?
|
Решение |
m = 60 кг
t1г = 80 °С
t1х = 20 °С
t2см = 40 °С
|
Анализ условия задачи показывает. что в теплообмене участвуют два тела. Поэтому уравнение теплового баланса имеет следующий вид:
Qх + Qг = 0
Qх = cmх(t2см - t1х) - количество теплоты, полученное холодной водой.
Qг = cmг(t2см - t1г) - количество теплоты, отданное горячей водой.
|
Тогда cmх(t2см - t1х) + cmг(t2см - t1г) = 0
Упростим уравнение поделив левую и правую части уравнения на с
mх(t2см - t1х) + mг(t2см - t1г) = 0
Известно, что необходимо получить 60 кг воды, значит:
mх + mг = m
Откуда mх = m - mг
Поэтому
(m - mг)(t2см - t1х) + mг(t2см - t1г) = 0
m t2см - mt1х - mг t2см + mг t1х + mг t2см - mг t1г = 0
m t2см - mt1х + mг t1х - mг t1г = 0
mг (t1х - t1г) = m (t1х - t2см)
В алюминиевый калориметр массой 140 г налили 250 г воды при температуре 15 °С. После того как брусок из свинца массой 100 г, нагретый до 100 °С, поместили в калориметр с водой, там установилась температура 16 °С. Составьте уравнение теплового баланса и определите удельную теплоемкость свинца.
Дано:
сc - ?
|
Решение |
mk = 140 г
mв = 250 г
mс = 100 г
t1к = t1в = 15 °С
t1с = 100 °С
t2см = 16 °С
|
В теплообмене участвуют три тела. Значит,
Qk + Qв + Qc = 0 - уравнение теплового баланса.
Qk = ckmk(t2см - t1k) - количество теплоты, полученное калориметром.
Qв = cвmв(t2см - t1в) - количество теплоты, полученное водой.
Qс = cсmс(t2см - t1с) - количество теплоты, отданное свинцовым бруском
Анализ формул показывает необходимость выяснить из справочных таблиц «Тепловые свойства веществ» удельные теплоемкости воды и алюминия.
Из уравнения теплового баланса имеем:
Qc = -(Qk + Qв)
Откуда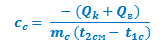 
|
| 
Кирхгоф Густав Роберт — немецкий физик, член Берлинской Академии Наук (1875), член-корреспондент Петербургской Академии Наук (1862).