Система тел. Закон сохранения импульса.
В механике часто встречаются задачи, когда необходимо одновременно рассматривать несколько тел, движущихся по-разному. Например, задачи о соударении тел, об отдаче огнестрельного оружия, где и снаряд и пушка начинают двигаться после выстрела, и т. д. В этих случаях говорят о движении системы, тел: системы двух соударяющихся тел, системы пушка - снаряд и т. п.
Между телами системы действуют некоторые силы. В системе соударяющихся тел - это силы упругости, в системе пушка - снаряд - силы давления пороховых газов.
Кроме сил, действующих со стороны одних тел системы на другие (внутренние силы), на тела могут действовать еще силы со стороны тел, не принадлежащих системе (внешние силы); например, на соударяющиеся бильярдные шары действуют еще сила тяжести и сила упругости стола. Однако в ряде случаев внешними силами можно пренебрегать. Так, при соударении катящихся шаров силы тяжести уравновешены для каждого шара в отдельности силами упругости и потому не влияют на их движение. В таком случае систему можно считать замкнутой.
Замкнутая система - система тел, для которой равнодействующая внешних сил равна нулю.
Рассмотрим систему, состоящую из двух шаров массой m1 и m2, движущихся навстречу друг другу с начальными скоростями v10 и v20 соответственно. Будем считать систему замкнутой.
При столкновении шаров сила F21, которая действует на первый шар со стороны второго по третьему закону Ньютона равна по модулю и противоположна по направлению силе F12 , действующей на второй шар со стороны первого:
(1)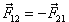
Заметим, что время действия сил одинаково.
Пусть v1 и v2 - скорости шаров после столкновения. Тогда выражения для соответствующих импульсов сил:
(2) 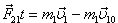
(3) 
Сложим почленно равенства (1) и (2)
(4)
(5) 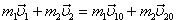
Заметим, что в правой части равенства содержится суммарный импульс системы в начальный момент времени, а в левой - сумма импульсов тел в произвольный момент времени после взаимодействия. Таким образом, при столкновении суммарный импульс системы сохраняется.
Геометрическая сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых движениях и взаимодействиях тел системы.
|